Теория Вероятностей - Контрольная работа №1 Вариант 8

Описание

Задание 1(Р39).
В ящике 10 деталей, среди которых 3 бракованных. Случайно извлекли 4 детали. Найти вероятность того, что среди них окажутся две бракованных.

Задание 2(790.Д6).
ОТК проверяет изделие на стандартность. Вероятность стандартности изделия равна 0,85. Найти вероятность того, что из двух проверенных изделий только одно стандартно. Ответ записать в виде десятичной дроби.

Задание 3(4Д1.Д6).
Три стрелка A, B, C стреляют по некоторой цели, делая не более одного выстрела. Вероятности попадания их при одном выстреле соответственно равны 0,7, 0,8, 0,9. Стрельбу начинает A. Если он промахнётся, то стреляет B. Если и B промахнётся, то стреляет C. Найти вероятность (в виде десятичной дроби) того, что цель будет поражена.

Задание 4(СС2.Д7).
При рентгеновском обследовании вероятность обнаружить туберкулёз равна 0,9. Вероятность принять здорового человека за больного равна 0,01. Доля больных туберкулёзом ко всему населению равна 0,001. Найти вероятность того, что человек здоров, хотя он признан больным при обследовании. Ответ округлить до 0,001.

Задание 5.
Стрельба продолжается до первого попадания, но не более 4-х выстрелов. Вероятность попадания при каждом выстреле равна 0,6. X – число израсходованных патронов. Найти (ответы вводить в виде десятичной дроби): а) (8Д.Б7) ряд распределения X; б) (40.Р7) функцию распределения F(x), в ответ записать F(1,5), F(3,5); в) (814); г) (684), ответ округлить до 0,01; д) (074) P(1,5 < X < 3,5).

Задание 6.
Дана плотность распределения случайной величины X:

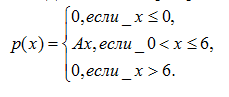
Найти: а) константу A; б) функцию распределения F(x), в ответе записать F(3); в)mx; г)Dx; д) P(2<X<4).

Задание7(А69).
Деталь, изготовленная автоматом, считается годной, если отклонение X её контролируемого размера от номинала не превышает 18 мм. Величина X распределена нормально, причём ax=9мм. Найти вероятность того, что деталь будет признана годной. Ответ округлить до 0,01.