Теория Вероятностей - Контрольная работа №11 Вариант 1

Описание

Задача 1
Подброшены две игральные кости. Найти вероятность того, что сумма выпавших очков равна пяти.

Задача 2
События А и В независимы. Вероятность наступления хотя бы одного из них равна 0,76, а ровно одного – 0,52. Найти Р(А) и Р(В), если Р(А) > Р(В). В ответ записать Р(А), а затем Р(В) в виде десятичной дроби.

Задача 3
Рабочий обслуживает три станка. Первый станок может требовать ремонта с веро-ятностью р1 = 0,2; второй – р2 = 0,3; а третий – р3 = 0,4. Найти вероятность того, что не более двух станков потребует ремонта. Ответ ввести в виде десятичной дроби.

Задача 4
Ключи К1, К2, К3 соединены по указанной схеме. Вероятность того, что они за-мкнуты равны 0,2; 0,4; 0,6. При включении в сеть цепь MN оказалась замкнутой. Найти вероятность того, что при этом ключи К2 и К3 были замкнуты, а К1 разомкнут.

Задача 5
Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,6. Случайные величины Y – число попаданий, Z – число промахов, X = |Y – Z|. Найти (все ответы вводить в виде десятичной дроби): а) ряд распре-деления Х; б) функцию распределения F(x), в ответ ввести F(1,5); в) mx; г) Dx;
д) Р(1,5<=Х <=2,5).

Задача 6
Случайная величина Х задана плотностью распределения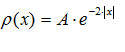. Найти (ответы вводить в виде десятичных дробей): а) константу А; б) функцию распре-деления F(x), в ответ записать F(–1), F(1), приняв е–2 = 0,135; в) mx; г) Dx; д) Р(–1<=Х<=1), ответ округлить до 0,001.

Задача 7
Деталь, изготовленная автоматом, считается годной, если отклонения Х ее контро-лируемого размера от проектного не превышает 15 мм. Величина Х нормальна mx = 0, aх = 10 мм. Сколько процентов годных деталей изготавливает автомат? Ответ округлить до целых.