Гидравлика - Контрольная работа Вариант №10

Описание

Задача № 2.
Автоклав объёмом V наполнен водой и закрыт герметично. Определить повышение давление в нём Δp при увеличении температуры воды на Δt, если коэффициент температурного расширения βt=0.00018°C-1, а коэффициент сжимаемости βp=0.42×10-9 Па-1. Изменением объёма автоклава пренебречь. Данные, необходимые для решения задачи, взять из табл. 3.
Дано: V=1.7 м3; Δt=54°C; βt=0.00018°C-1; βp=0.42×10-9 Па-1.
Найти: Δp.

Задача № 11.
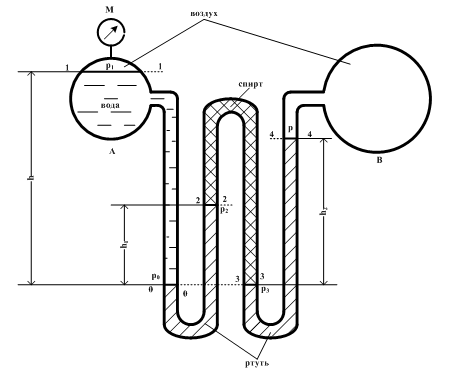
Найти давление p воздуха в резервуаре B, если избыточное давление на поверхности воды в резервуаре А равно М, разности уровней ртути (δ=13.6) в двух коленном дифференциальном манометре h1 и h2, а мениск ртути в левой трубке манометра ниже уровня воды на h. Пространство между уровнями ртути в манометре заполнено спиртом (δ=0.8).
Дано: h=1.05 м; h1=240 мм; h2=275 мм; pм=55 кПа; δ1=13.6 т/м3; δ2=0.8 т/м3
Найти: p.


Задача № 42.
Определить диаметр трубопровода, по которому подаётся жидкость Ж с расходом Q, из условия получения в нём максимально возможной скорости при сохранения ламинарного режима. Температура жидкости t=20°C.
Дано: Ж – бензин; Q=3.5 л/с.
Найти: d.

Задача № 52.
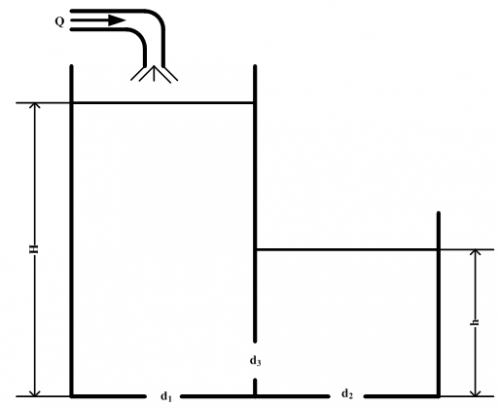
В бак, разделённый перегородкой на два отсека, поступает расход воды Q. В дне каждого отсека имеются одинаковые отверстия диаметром d1 и d2, а в перегородке – отверстие диаметром d3. Определить расход через донные отверстия Q1 и Q2.
Дано: Q=44 л/с; d1=d2=75 мм; d3=125 мм.
Найти: Q1, Q2


Задача № 60.
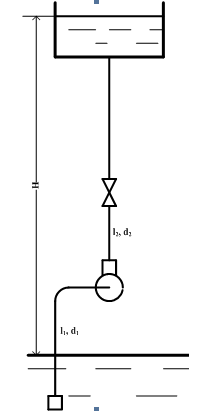
Центробежный насос с заданной при числе оборотов n=900 мин-1 характеристикой подни-мает воду на высоту Hг по трубопроводам l1, d1 (λ1=0.02) и l2, d2 (λ2=0.025). Определить подачу Qн насоса при работе его с числом оборотов n=900 мин-1. Сравнить потребляемые насосом мощности при уменьшении его подачи на 25% дросселированием задвижкой или уменьшением числа оборотов. Местные сопротивления учтены эквивалентными длинами, включенные в заданные длины труб.
Дано: Hг=7 м; l1=17 м; d1=0.27 м; l2=95 м; d2=0.22 м.
Найти: Qн.


Задача № 69.
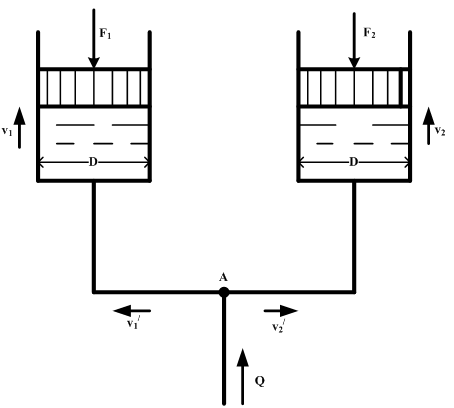
Перемещение поршней гидроцилиндров с диаметром D=25 см осуществляется подачей рабочей жидкости (ν=1.5 см2/с, γ=14000 Н/м3) по трубам 1 и 2 одинаковой эквивалентной длины l=20 м и диаметром d=5 см. определить силу F2, при которой скорость второго поршня была бы в два раза больше скорости первого поршня. Расход в магистрали Q, первый поршень нагружен силой F1.
Указание. На перемещение поршней затрачивается одинаковый суммарный напор (считая от точки А).
Дано: F1=9.6 кН; Q=10.5 л/с.
Найти: F2.


Литература.